Before we calculate our Latitude (in the next post in this series) we have one vital concept to understand.
The Earth revolves around the Sun. It takes about 365 days to return to the same point, relative to the Sun.
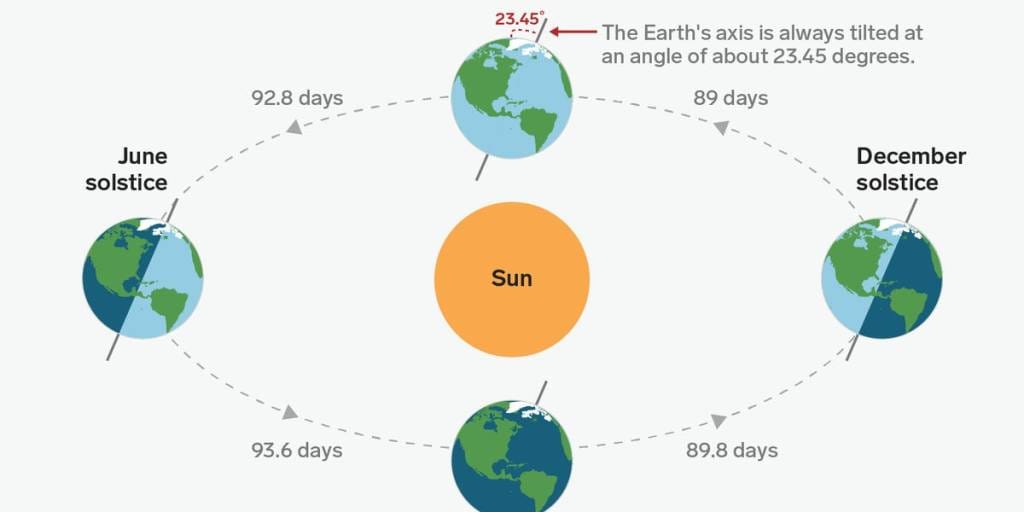
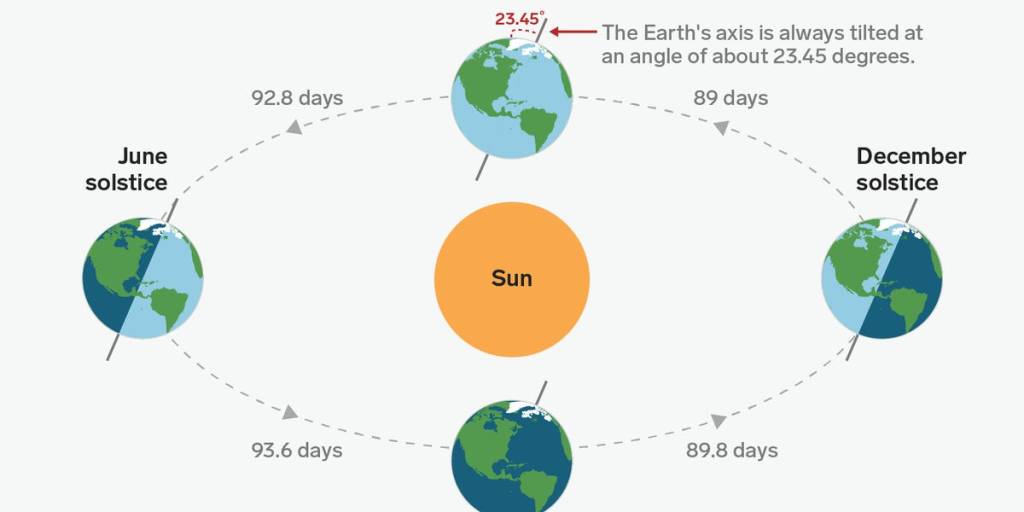
We are also tilted at an angle to the Sun and this gives us our Seasons. Right now we are in June so it’s the Southern Winter. As this diagram shows, we are further away from the Sun than in 6 months time; our Summer.
However, we are interested in Earth-bound Navigation. In fact, that is an extension of Earth-bound Astronomy, as traditional navigation – historically and even today – involves Astronomy.
So it is perfectly valid for us to consider the Earth as sitting upright in space with North pointing straight up. And so it’s the Sun who is at the Angle relative to us.
Earth-Centred View
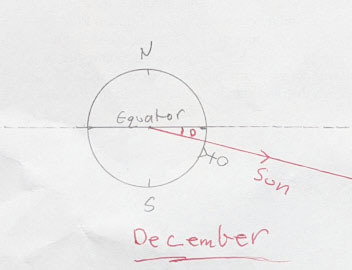
As per the earlier post, we look at the Earth from the side, with our Equator slicing through the middle and me standing here at home, about 1/3 of the way down (South) from the Equator.
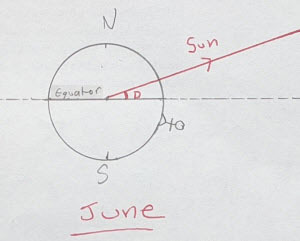
That red line is going from the centre of the Earth to the Sun. The Sun is huge but a long, long way away.
The key item here is that angle, marked with the red D. The Equator is a line (a plane, actually), and we can extend it into space and so create the Celestial Equator (the dotted line).
In this model the Earth is also stationary and the Celestial Equator doesn’t change. Everything else spins around us.
That angle, D, is very important. It is called the Sun’s Declination. If you look back, you’ll see it’s the equivalent to the Sun’s celestial latitude. The Declination is given in degrees North (like here) or South.
The Sun’s Declination changes over the year. In fact it’s changing, by tiny amounts, continuously. If we jump to our Summer – 6 months later – we now have this:
The angle D (Declination) has now changed. It is also South.
One other key idea: the Sun’s Declination is the same for every point on the Earth at the same time. To be clear, I mean ‘now’ it’s 4:36 pm Melbourne time, so that’s 5:36 am in London. A navigator in London and Melbourne would find the Sun’s Declination to be exactly the same value ‘now’.
Begs the question – how do you find the Sun’s Declination at a given date and time?
The same way that Lt James Cook did in the 1770s. A book.
The Book
It’s called The Nautical Almanac and available for free – as a PDF – on line. It is a bunch of tables and calculated for a given year. Of course there’s apps, but I think you’ll find most sailors carry a printed Almanac on board too.

It has a list of different values, for a given Date and Time. The one of interest for us is the Sun’s Declination.
Another key item: the Almanac has all times in UTC aka Greenwich. So you either have a clock set to this (which is what Cook did) or you simply convert your local clock’s time to UTC.
So, for 4:36 pm on Tues June 2nd (Melbourne) that would be 6:36 am UTC (same date). As an aside London is in ‘daylight savings’ aka summer time now, so 1 hour different from UTC.
We go to the Almanac and find the page with June 2nd 2020 on it. It has lots of other data, but we are after the Sun’s Declination for that UTC date and time.
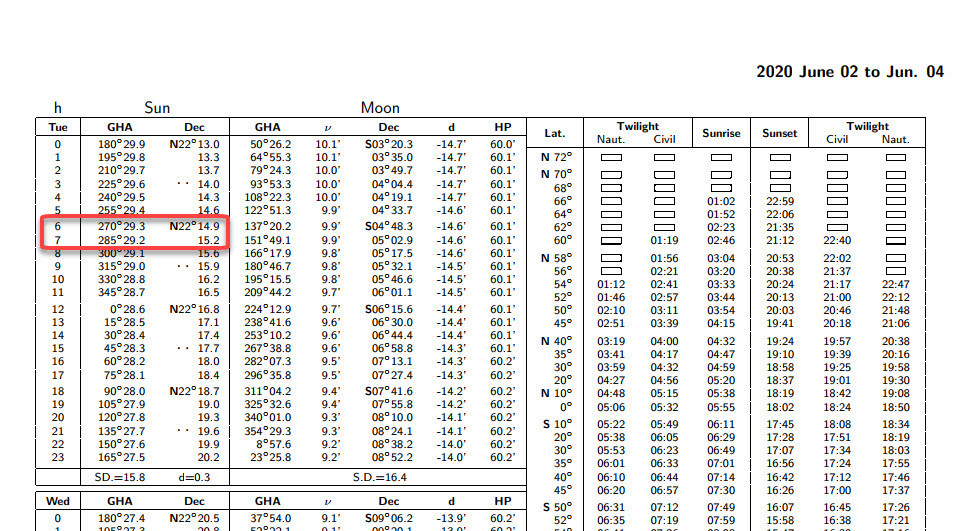
As you can see it shows hourly values (h). 6:36 UTC is pretty much halfway between 6 and 7 am, so we can pick the Declinations for 6 and 7 (22 degrees 14.9 minutes and 22 degrees 15.2 minutes North, respectively) and just average them.
It comes in at 22 degrees 15 minutes North. 22° 15’ N. In the next post in this series, we’ll see this Declination is vital for calculating our Latitude.
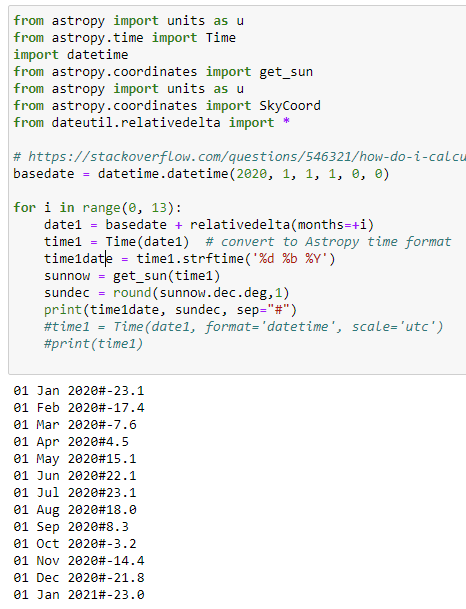
So how does it change over the Year? A quick [*cough*, see below] Python program to calculate it for the first of each month, shows:
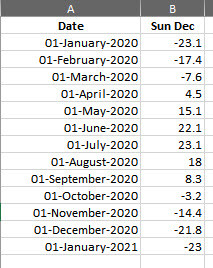
We will definitely return to what all means a bit later; after closing out the Navigation/Latitude part.
Behind the Scenes: ‘Quick’ Python Program
This took about 2 hours. I had to learn how to add ‘1 month’ to a date as well as how to get it to show the dates in a nice format.